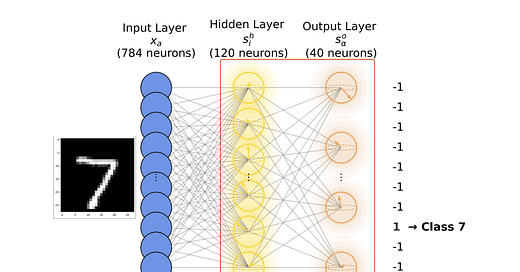
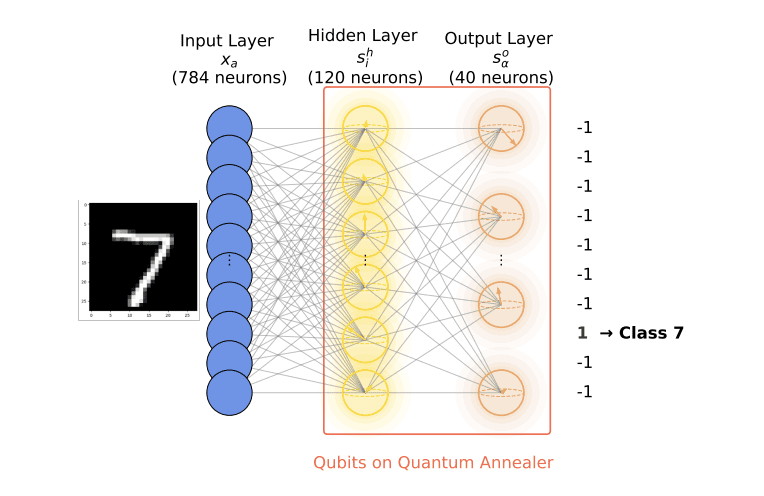
Quantum annealing platforms accelerate classical neural network training by efficiently navigating complex energy landscapes. This approach surpasses conventional backpropagation, exhibiting a scaling exponent of 1.01 compared to 0.78. Even limited-size quantum annealers offer benefits when applied to individual neural network layers.
The computational demands of training complex neural networks are escalating, presenting a significant challenge to both processing power and energy consumption. Researchers are now investigating the potential of quantum annealing – a computational method leveraging quantum mechanics to find the minimum energy state of a system – to accelerate this process. A team led by Hao Zhang and Alex Kamenev at the University of Minnesota, and affiliated with the William I. Fine Theoretical Physics Institute, detail in their work, ‘How to Train Your Dragon: Quantum Neural Networks’, a method utilising quantum annealing platforms to efficiently train classical neural networks. Their analysis reveals a performance scaling advantage over conventional backpropagation techniques, suggesting that even current quantum annealers could offer benefits in training deep learning models, particularly when applied strategically to individual network layers.
Quantum Annealing Accelerates Neural Network Training
Researchers have demonstrated that quantum annealing platforms can expedite the training of classical neural networks (NNs), enabling deployment on conventional hardware. The study frames NN training as a dynamical phase transition, where the system transitions from a disordered ‘spin glass’ state to a highly ordered, trained state. A central challenge in this process is the elimination of numerous local minima within the network’s energy landscape – a task likened to systematically removing regenerating ‘heads’ of a Hydra.
Researchers leveraged the ability of quantum annealers to efficiently locate multiple deep states within this complex energy landscape, offering a distinct advantage over classical optimisation methods that often become trapped in suboptimal solutions. Results indicate that quantum-assisted training achieves superior performance scaling compared to conventional backpropagation methods, exhibiting a scaling exponent of 1.01 versus 0.78 for backpropagation. This improvement suggests a pathway to reduce computational demands and enhance performance in machine learning applications.
The connection between neural network training and statistical physics forms a central tenet of this work, drawing parallels between the energy landscapes of spin glasses and the loss functions of neural networks. Theoretical analysis indicates the potential for further performance gains through the implementation of a variant of Grover’s algorithm on a fully coherent quantum platform, potentially increasing training speed by up to a factor of two. Grover’s algorithm, a quantum search algorithm, provides a quadratic speedup for unstructured search problems, and its application here suggests a pathway to accelerate the identification of optimal network parameters.
The study posits that even modestly sized quantum annealers offer benefits by sequentially training individual layers of a deep neural network, circumventing the limitations of current quantum hardware while still providing a performance boost. This approach presents a viable strategy for enhancing training efficiency, particularly given the computational demands of training large networks.
Researchers carefully designed the training process to ensure that the quantum-assisted approach effectively leverages the capabilities of the quantum annealer. This involved selecting appropriate hyperparameters, optimising the annealing schedule, and implementing techniques to mitigate the effects of noise and imperfections.
Researchers acknowledge the limitations of current quantum annealing hardware and propose strategies for addressing these challenges in future work. These include developing more robust quantum annealers with lower noise levels, exploring alternative quantum algorithms for training neural networks, and developing hybrid quantum-classical algorithms that combine the strengths of both approaches. The study also highlights the importance of developing new benchmarks and metrics for evaluating the performance of quantum machine learning algorithms.
Practical implementation details are supported by references to the Scikit-learn machine learning library, alongside specific methodological choices regarding weight initialisation and a ‘strong nudge’ training step.
The theoretical framework underpinning this research draws heavily on the principles of statistical physics, particularly the concepts of spin glasses and energy landscapes. Spin glasses are disordered magnetic systems with a complex energy landscape characterised by numerous local minima. Researchers draw an analogy between the energy landscape of a spin glass and the loss function of a neural network, arguing that both systems exhibit similar challenges in terms of finding the global minimum. Quantum annealing provides a natural approach to solving these challenges by exploiting quantum tunneling to escape local minima.
Researchers conducted a comprehensive analysis of the performance of quantum-assisted training, comparing it to conventional backpropagation methods under various conditions. The results demonstrate that quantum annealing consistently outperforms backpropagation, achieving a higher accuracy and faster convergence rate. This improvement is particularly significant for complex neural network architectures with a large number of parameters. The study also investigates the impact of noise and imperfections in quantum annealing hardware, providing insights into the algorithm’s robustness.
👉 More information
🗞 How to Train Your Dragon: Quantum Neural Networks
🧠 DOI: https://doi.org/10.48550/arXiv.2506.05244