BlueQubit Demonstrates Heuristic Quantum Advantage with Peaked Circuits
The quest for quantum supremacy, demonstrating a quantum computer can outperform the best classical algorithms, just took a potentially significant step forward. Researchers at BlueQubit have achieved what they term “heuristic quantum advantage” using specifically designed quantum circuits featuring a “peaked” structure. This new approach focuses not just on raw computational power, but on crafting problems where classical simulation becomes exponentially difficult, even with optimized methods. By meticulously analyzing the memory and time required for classical simulations, the team has found evidence suggesting their circuits push the limits of current classical capabilities, hinting at a pathway towards practical quantum advantage, and a future where quantum computers can tackle currently intractable problems.
Bond Dimension Scaling with Circuit Depth
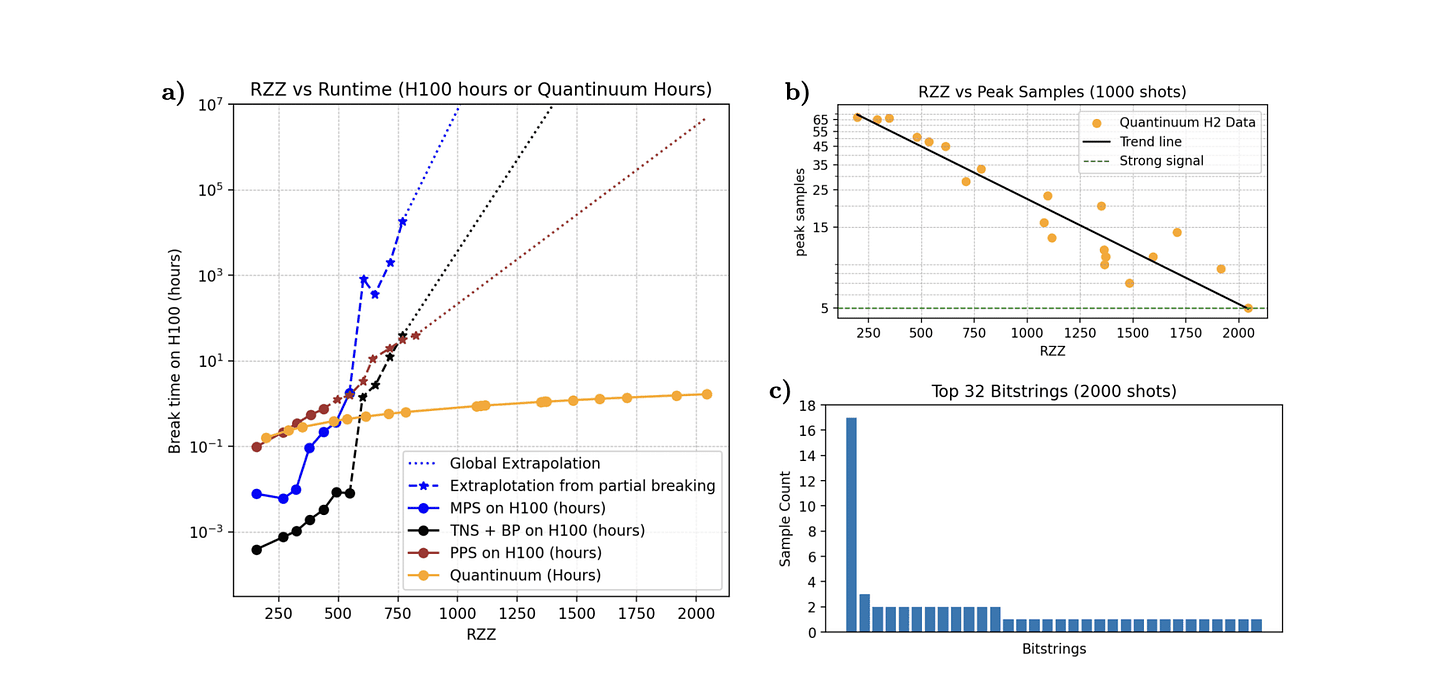
A critical aspect of BlueQubit’s approach to demonstrating heuristic quantum advantage lies in meticulously characterizing the computational cost, both in terms of memory and time, required for classical simulation, specifically using Matrix Product State (MPS) methods. Their research details how the necessary bond dimension, denoted as χ (chi), scales with increasing circuit depth, a key indicator of the simulation’s difficulty. The team observed an exponential growth in χ as circuit depth increases, mirroring expectations for random quantum circuits, until reaching a saturation point, χsat, approximately 108 for the system sizes tested. However, their peaked circuits appear to push beyond this saturation, with extrapolated values of χbreak, the bond dimension at which the MPS simulation “cracks” and loses accuracy, exceeding the maximum bond dimension used in their experiments (χ = 5000). This suggests the peaked structure genuinely increases the inherent difficulty for classical simulation.
To determine χbreak when a circuit remains “uncracked” across all tested bond dimensions, BlueQubit employs an automated fitting procedure, assuming a linear relationship in log χ, weighted towards larger values, and rejecting fits lacking sufficient correlation (r2 < 0.8) or exhibiting negative slopes. This extrapolation is performed on five instantiations per circuit depth, reporting both the average and standard deviation of χbreak in logarithmic scale, acknowledging the stochasticity introduced by the training process. Beyond memory requirements, the research also addresses the time, T, required for simulation. They found the runtime is dominated by gate application (scaling as χ2) and subsequent Singular Value Decomposition (SVD, scaling as χ3), leading to a fitted functional form of T/RZZ ∼ aχ2 + bχ3, where RZZ represents the two-qubit gate count. This allows for extrapolation of the total runtime needed for the deepest circuits, a crucial element in assessing the feasibility of classical simulation as quantum circuit complexity increases.
Their findings, demonstrate an exponential increase in both χbreak and the solution time, Tbreak, with circuit depth, providing a compelling argument that their peaked circuits are indeed presenting a significant challenge to classical computational resources and hinting at a pathway towards practical quantum advantage. The ability to accurately model and extrapolate both the memory and time costs is paramount, as it allows BlueQubit to estimate the resources needed to simulate even deeper circuits, potentially revealing the point at which classical simulation becomes entirely intractable, thus solidifying the claim of quantum supremacy.
Source: https://arxiv.org/pdf/2510.25838